The story of FLARE: Fast Low-rank Attention Routing Engine

Attention, the core mechanism of transformers, becomes prohibitively expensive at large sequence lengths. This post explains the ideas behind FLARE, an attention operator designed to retain global communication while scaling to million-token regimes on a single GPU.

Rather than focusing on architectural novelty for its own sake, the goal is to understand attention as a communication operator and ask a simple question: can we keep the benefits of global message passing without paying the full quadratic cost?

This post complements our latest paper (arXiv:2508.12594). See my dissertation proposal talk on this topic!

FLARE overview

Why this problem is hard

Attention is now used across language, vision, and scientific machine learning. The scaling bottleneck appears everywhere. For a sequence of $N$ tokens, standard self-attention requires $O(N^2)$ compute and memory, which quickly becomes impractical beyond tens of thousands of tokens.

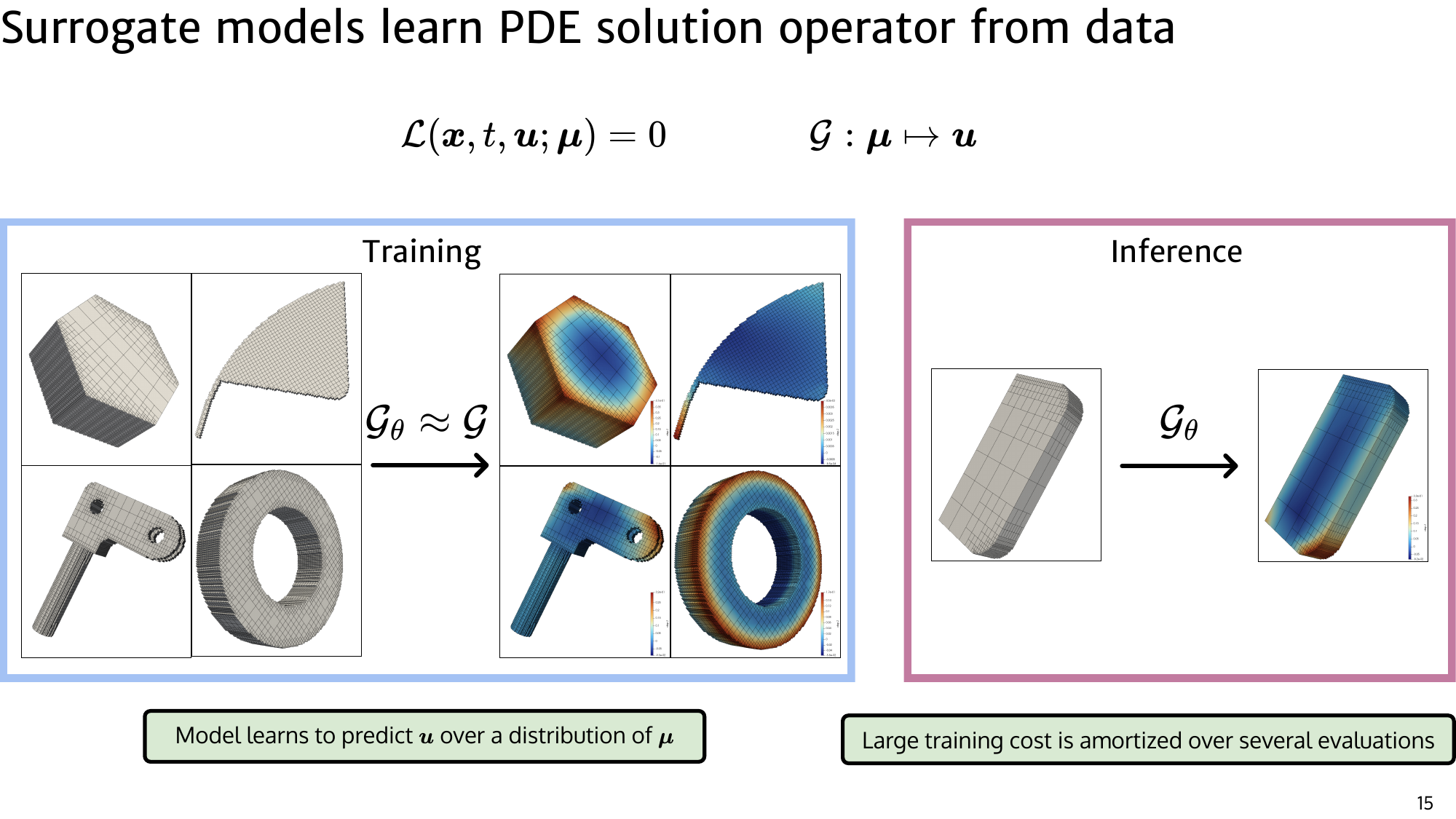
We are particularly motivated by partial differential equation (PDE) surrogate modeling, one of the most demanding settings for attention:

  • Inputs are large and geometry dependent.
  • Meshes are often unstructured, so ordering tricks are unreliable.
  • Accurate predictions require long-range interactions across the domain.

Linear attention methods reduce cost but often struggle to match accuracy in these regimes. The challenge is not just scaling attention, but scaling it without losing expressive global communication.

PDE surrogate modeling

For a PDE

$$ \mathcal{L}(\boldsymbol{x}, t, \boldsymbol{u}; \boldsymbol{\mu}), \quad \boldsymbol{x}\in\Omega, $$
we view learning as approximating a solution operator \(\mathcal{G}\) that maps parameters to fields:
$$ \boldsymbol{u}(\boldsymbol{x})=\mathcal{G}(\boldsymbol{\mu})(\boldsymbol{x}). $$
In practice, we train on many \(\boldsymbol{\mu}\to \boldsymbol{u}\) pairs and require generalization to unseen \(\boldsymbol{\mu}\). In the slide below, \(\boldsymbol{\mu}\) is effectively the geometry \(\Omega\), and the target is a strain field on unseen domains.

Slide 15: PDE surrogate motivation

Token mixing in transformers

A transformer block is conceptually two operations:

  1. pointwise nonlinear transforms (MLPs),
  2. global message passing (self-attention).

Slide 16: Transformer ingredients for PDEs

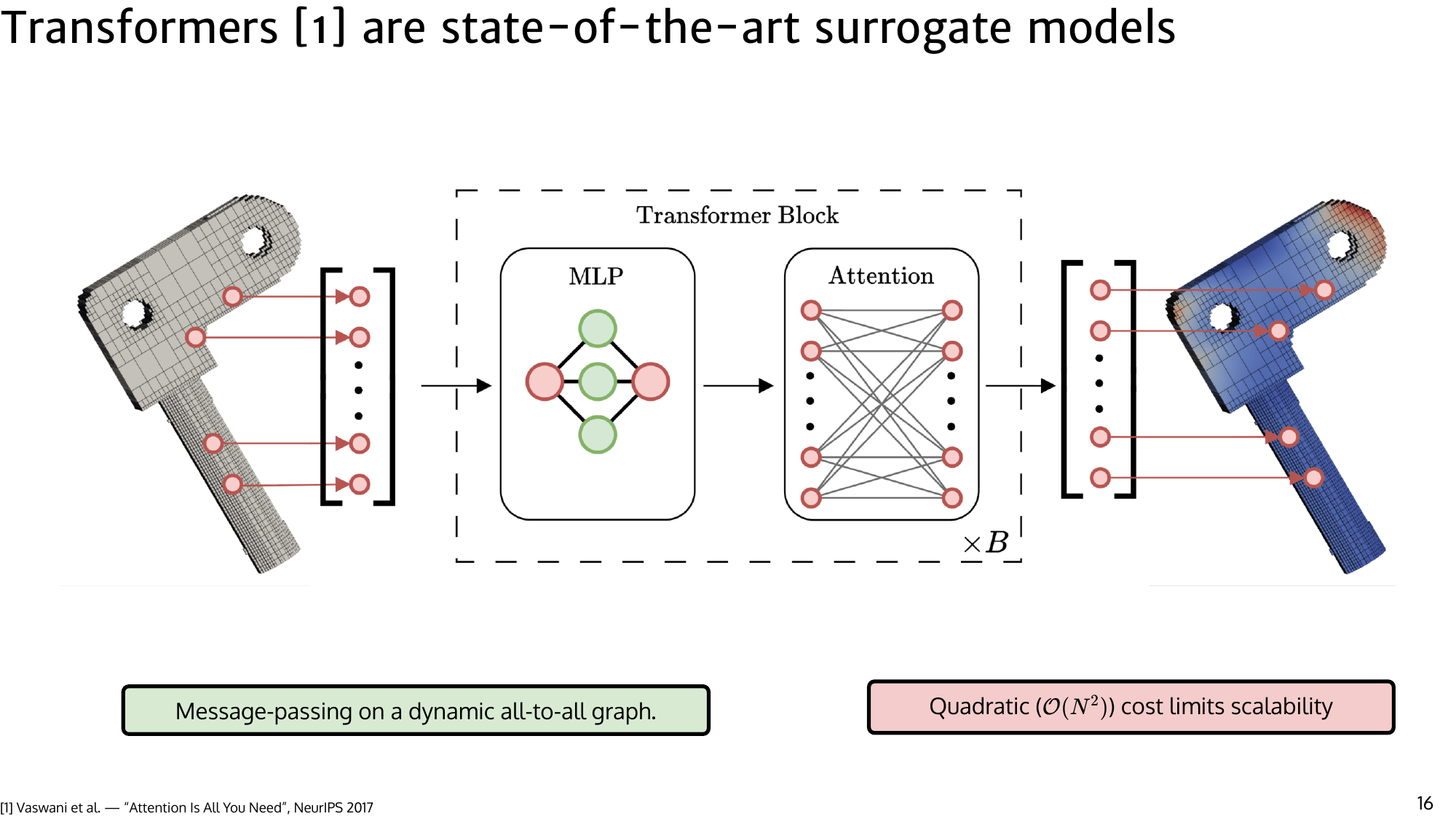
For PDE data, we avoid token clustering heuristics and treat each mesh point as a token. Standard attention computes, for each output token, a distribution over all inputs:

$$ y_n = \sum_m \frac{\exp\left(q_n^T \cdot k_l \right)}{\sum_l \exp \left(q_n^\top \cdot k_l \right)} v_l $$

This all-to-all routing is powerful but expensive. At million-token scale, even a single forward-backward pass can take tens of seconds. The goal is to keep global communication while reducing the number of messages that must be exchanged.

Slide 17: Quadratic self-attention bottleneck

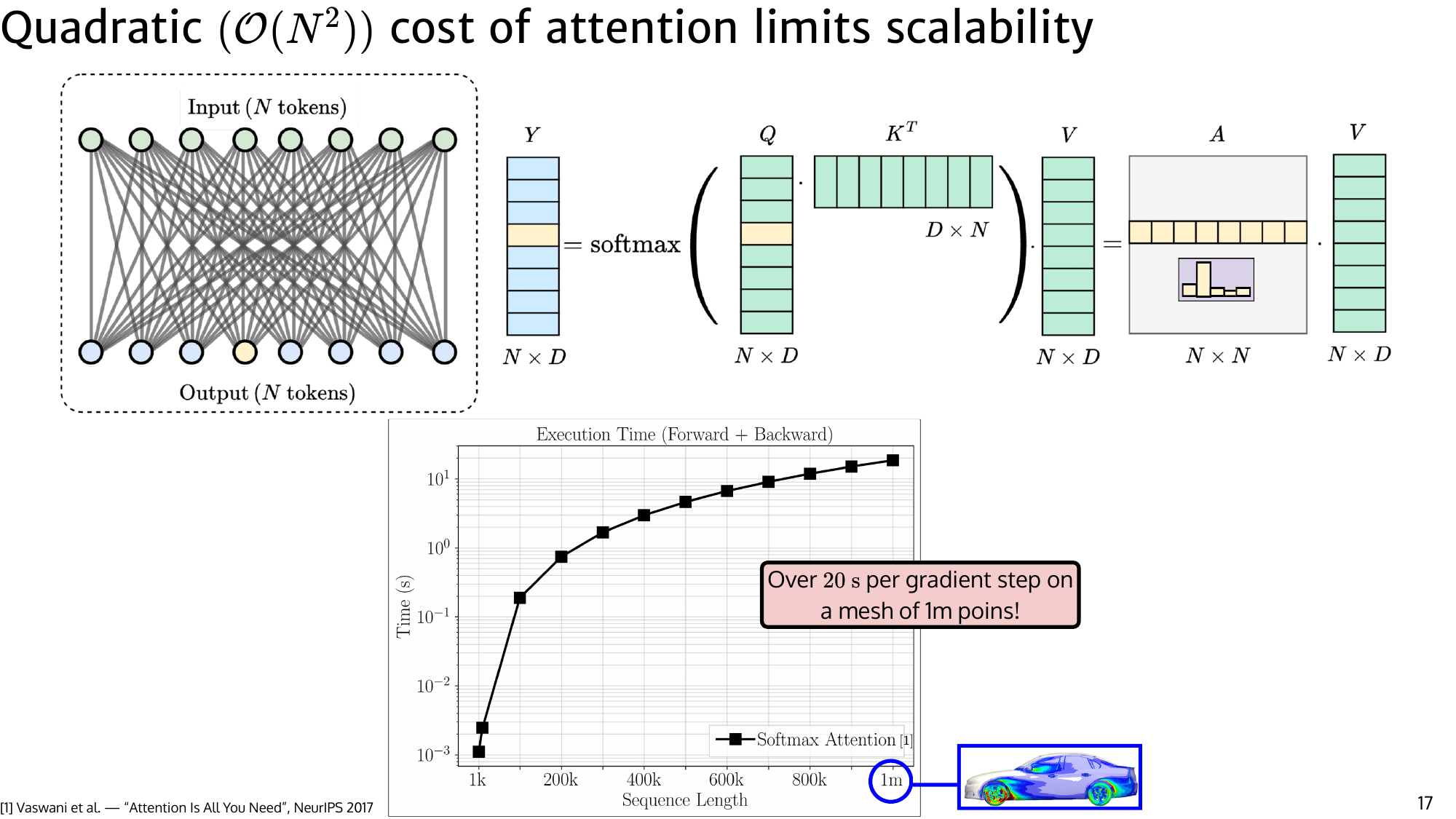
Why global communication still matters

In many physical systems, forward operators are local, but solution operators are effectively dense. A model that communicates only locally will miss long-range dependencies that determine the final field.

However, physical signals are often smooth at resolved scales. Smoothness implies redundancy: nearby tokens frequently carry similar information for distant targets. This suggests we may not need to send separate messages from every token if we can aggregate similar ones.

This observation motivates a low-rank communication view of attention.

Slide 18: Sparse forward operator vs dense solution operator

Are $N^2$ messages really necessary?

Physical fields are usually smooth at resolved scales. Smoothness means many high-frequency modes are weak; in a fully resolved signal, there is redundancy. So if two nearby source points carry nearly the same information for a far target point, we should be able to route one combined message instead of two separate ones.

Navier-Stokes spectrum

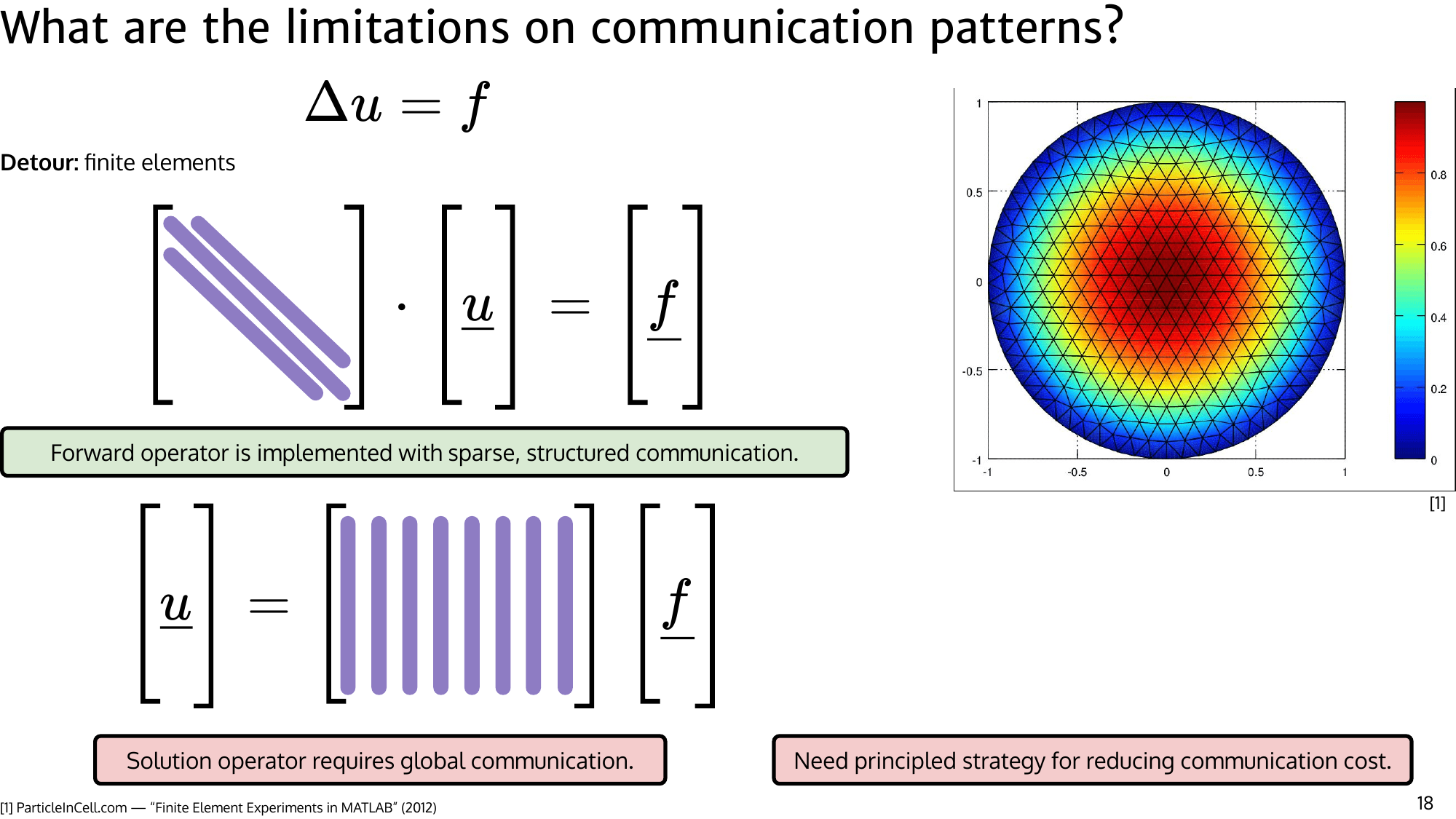
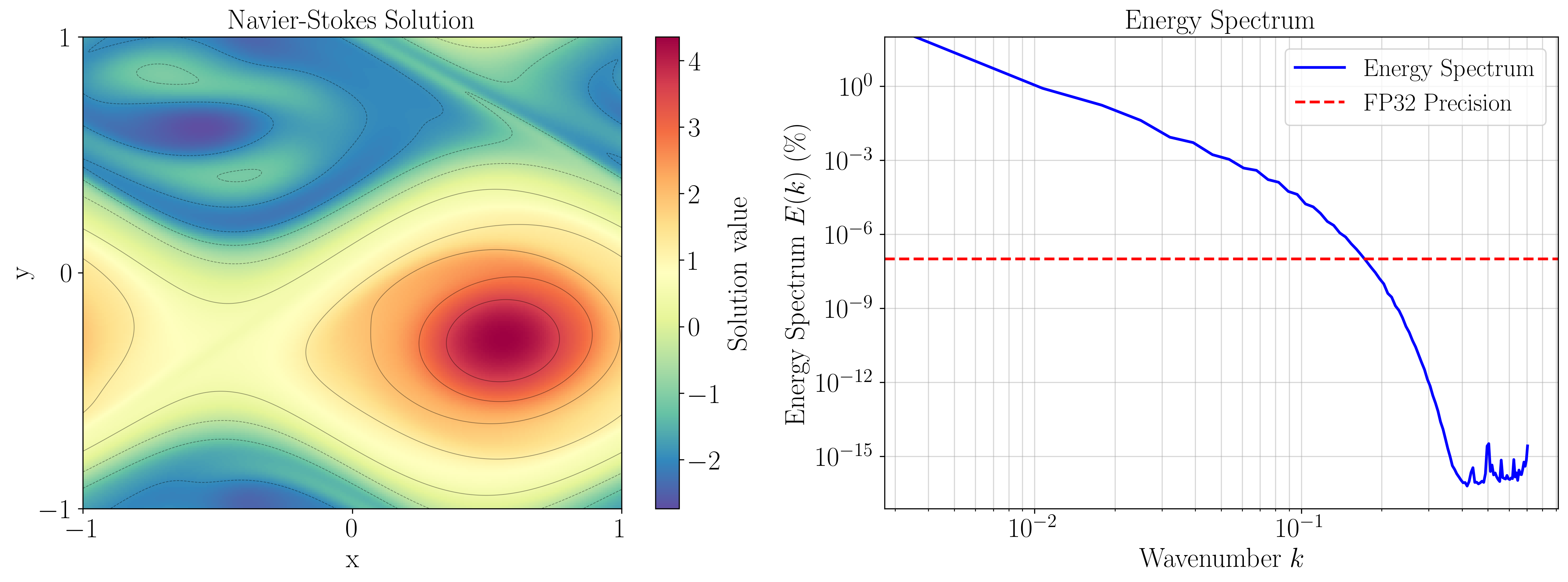
The core FLARE contribution is to operationalize this physics-guided redundancy into a sequence-agnostic attention mechanism that remains general-purpose.

FLARE

How we got to FLARE

The starting point was a simple systems question: what actually makes attention expensive?

Attention can be interpreted as a routing mechanism where each token decides how to combine information from all others. The quadratic cost comes from explicitly computing all pairwise interactions, even when many of those interactions are redundant.

From a physics perspective, many solution operators exhibit low effective dimensionality. Spectral decay in physical fields suggests that long-range interactions can often be captured through a smaller set of communication pathways.

This led to the idea of introducing a small set of latent routing tokens that act as intermediaries. Instead of every token talking to every other token directly, tokens communicate through these shared hubs. The challenge was designing this mechanism so that it remains global, interpretable, and easy to optimize.

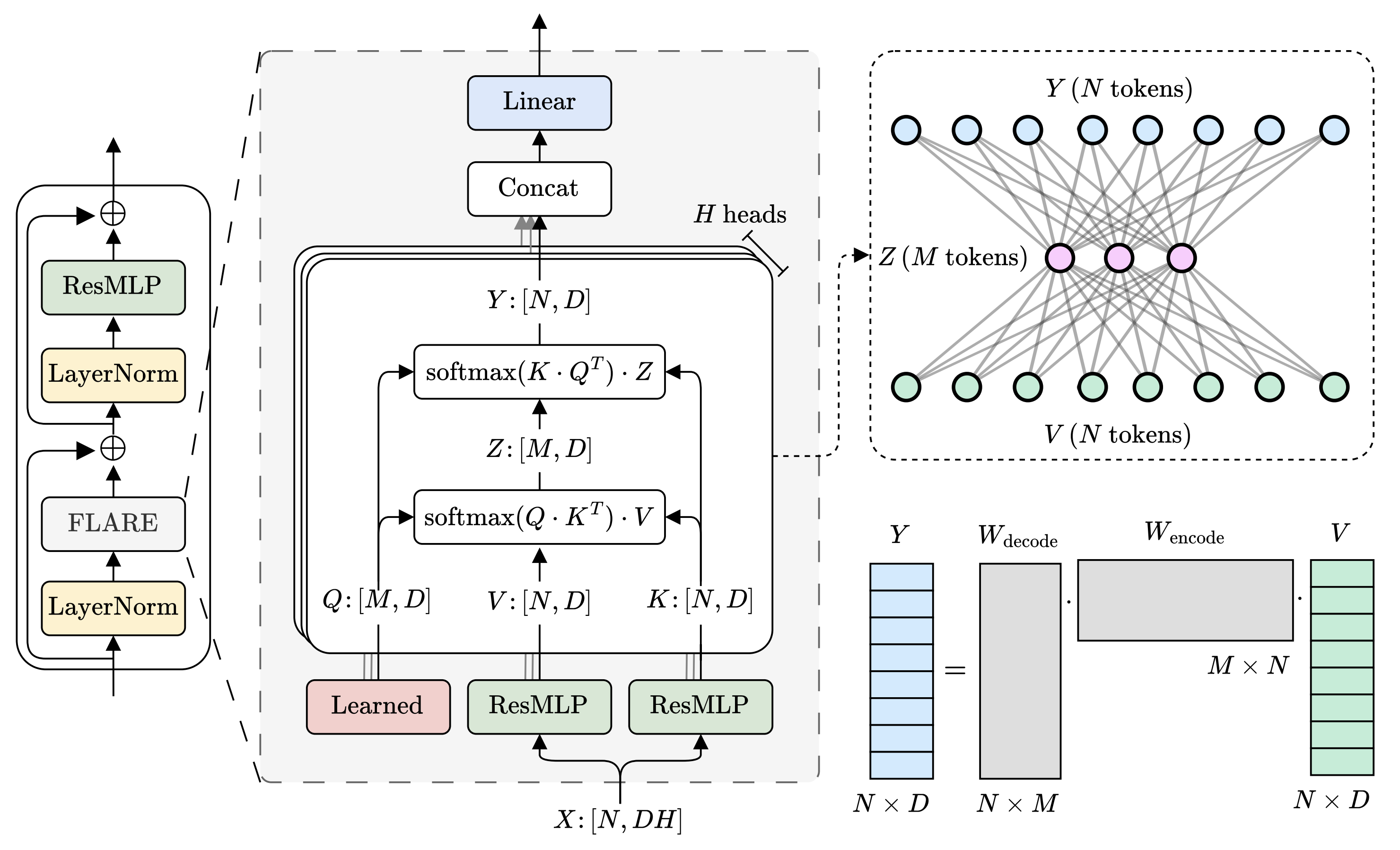
FLARE Method

FLARE implements global communication through a two-step gather–scatter mechanism, but it does so using standard, highly optimized attention primitives.

Scaled dot-product attention (SDPA)

The basic attention primitive is scaled dot-product attention. Given queries $Q \in \mathbb{R}^{N_q \times d}$, keys $K \in \mathbb{R}^{N_k \times d}$, and values $V \in \mathbb{R}^{N_k \times d_v}$, attention is

$$ \mathrm{SPDA}(Q,K,V) = \mathrm{softmax}!\left(\frac{Q \cdot K^\top}{\sqrt{d}}\right)V. $$

Naively, this suggests computing the score matrix $S = Q \cdot K^\top \in \mathbb{R}^{N_q \times N_k}$, applying softmax, and then multiplying by $V$. That approach is expensive because it materializes an $N_q \times N_k$ matrix.

Modern frameworks provide SDPA as a fused kernel that computes the same result without materializing the full attention-weight matrix in memory. In PyTorch, torch.nn.functional.scaled_dot_product_attention is the standard entry point, and under the hood it can dispatch to fused implementations (for example FlashAttention-style kernels) that stream over blocks of $K,V$ and maintain the softmax normalization online. Practically, SDPA lets you use the standard attention math while keeping memory use close to $O((L_q+L_k)d)$ rather than $O(L_qL_k)$.

FLARE is built to use SDPA twice: once to gather information into a small latent set, and once to scatter it back.

Step 1: Gather (encode)

Introduce $M \ll N$ latent tokens per head. Let $Q_h \in \mathbb{R}^{M \times d}$ be latent queries, and let $K_h, V_h \in \mathbb{R}^{N \times d}$ be token keys/values of head $h$. The gather step pools from the $N$ tokens into $M$ latents:

$$ Z_h = \mathrm{SDPA}(Q_h, K_h, V_h). $$

In matrix notation this is

$$ W_{\mathrm{enc}} = \mathrm{softmax}(Q_h \cdot K_h^\top) \in \mathbb{R}^{M \times N}, \qquad Z_h = W_{\mathrm{enc}} \cdot V_h. $$

Importantly, although $W_{\mathrm{enc}}$ is a useful conceptual object, SDPA computes $Z_h$ without explicitly materializing $W_{\mathrm{enc}}$.

Step 2: Scatter (decode)

Next, the latents broadcast information back to all $N$ tokens using the reverse affinity pattern:

$$ Y_h = \mathrm{SDPA}(K_h, Q_h, Z_h). $$

In matrix form,

$$ W_{\mathrm{dec}} = \mathrm{softmax}(K_h \cdot Q_h^\top) \in \mathbb{R}^{N \times M}, \qquad Y_h = W_{\mathrm{dec}} \cdot Z_h. $$

Combining both steps gives an implicit global communication operator:

$$ Y_h = (W_{\mathrm{dec}} \cdot W_{\mathrm{enc}}) \cdot V_h. $$

The product $W_{\mathrm{dec}} \cdot W_{\mathrm{enc}} \in \mathbb{R}^{N \times N}$ is a dense global mixing matrix, but its rank is at most $M$. FLARE therefore achieves global communication at $O(NM)$ cost per head (with $M \ll N$), and the SDPA kernels avoid ever forming the intermediate $N \times M$ or $M \times N$ attention matrices in memory.

Slide 20: FLARE in two steps

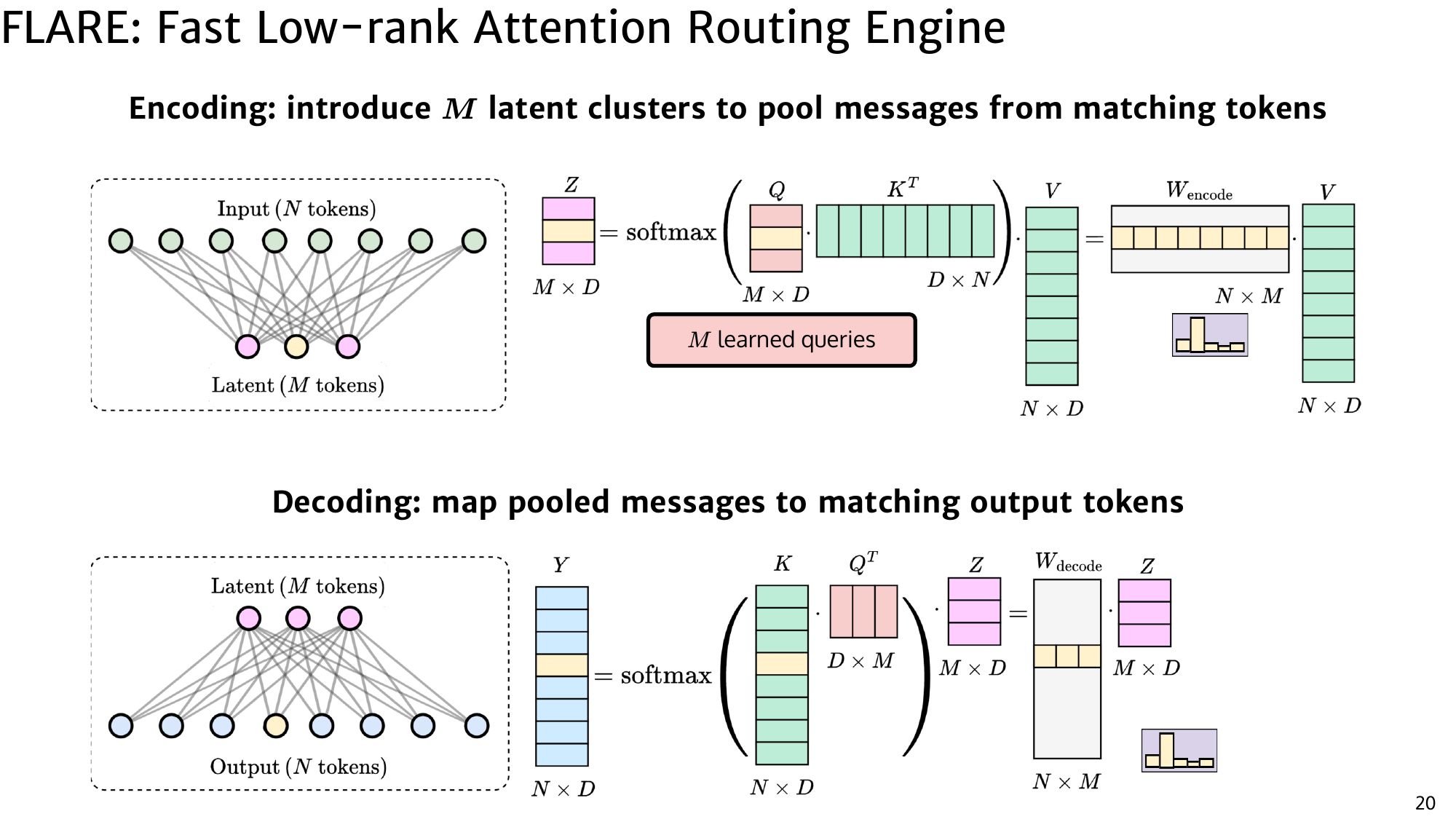
Minimal implementation

Below is the core mixer expressed directly with PyTorch SDPA. This is essentially the gather–scatter operator in a few lines.

from torch.nn.functional import scaled_dot_product_attention as SDPA

def flare_multihead_mixer(Q, K, V):
    """
    Args:
        Q: [H, M, D]          latent queries (per head)
        K: [B, H, N, D]       token keys
        V: [B, H, N, D]       token values

    Returns:
        Y: [B, H, N, D]       mixed token outputs
    """
    Qb = Q.unsqueeze(0)      # [1, H, M, D] to match SDPA batching

    # Gather: tokens -> latents
    Z = SDPA(Qb, K, V, scale=1.0)   # [B, H, M, D]

    # Scatter: latents -> tokens
    Y = SDPA(K, Qb, Z, scale=1.0)   # [B, H, N, D]

    return Y

The full FLARE block stacks this mixer with standard projection/MLP components: Slide 21: Low-rank token communication

And here are the scaling results: Slide 21: Low-rank token communication

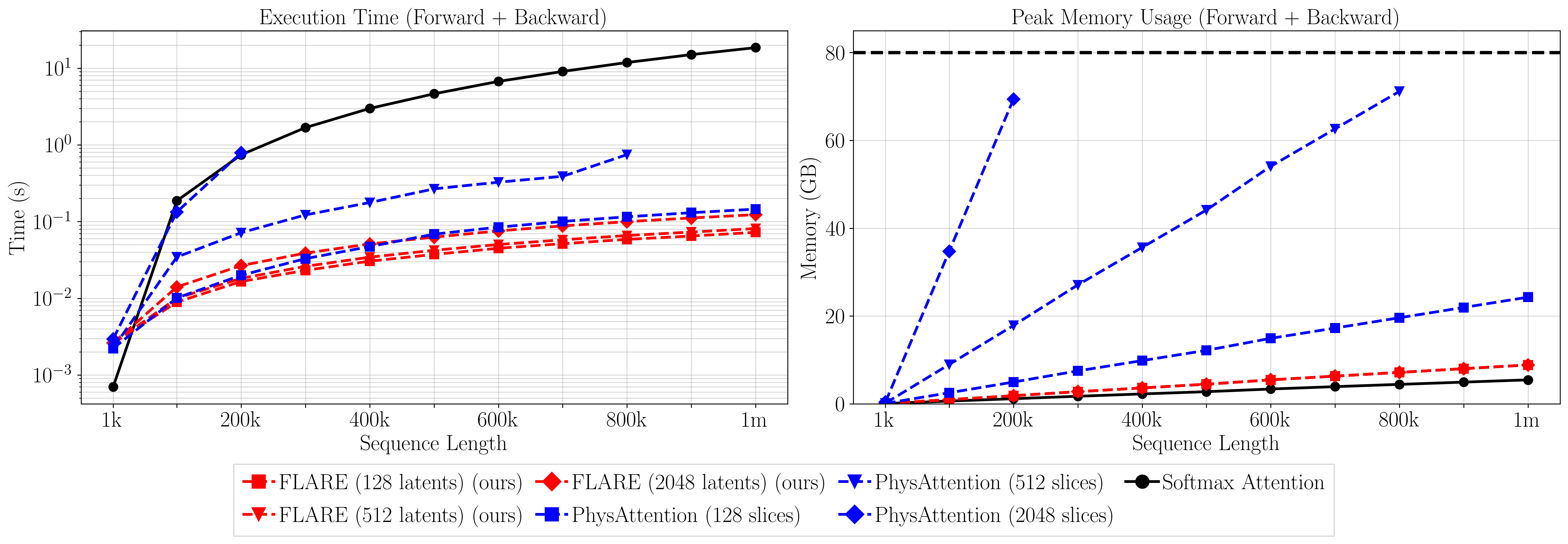
Results

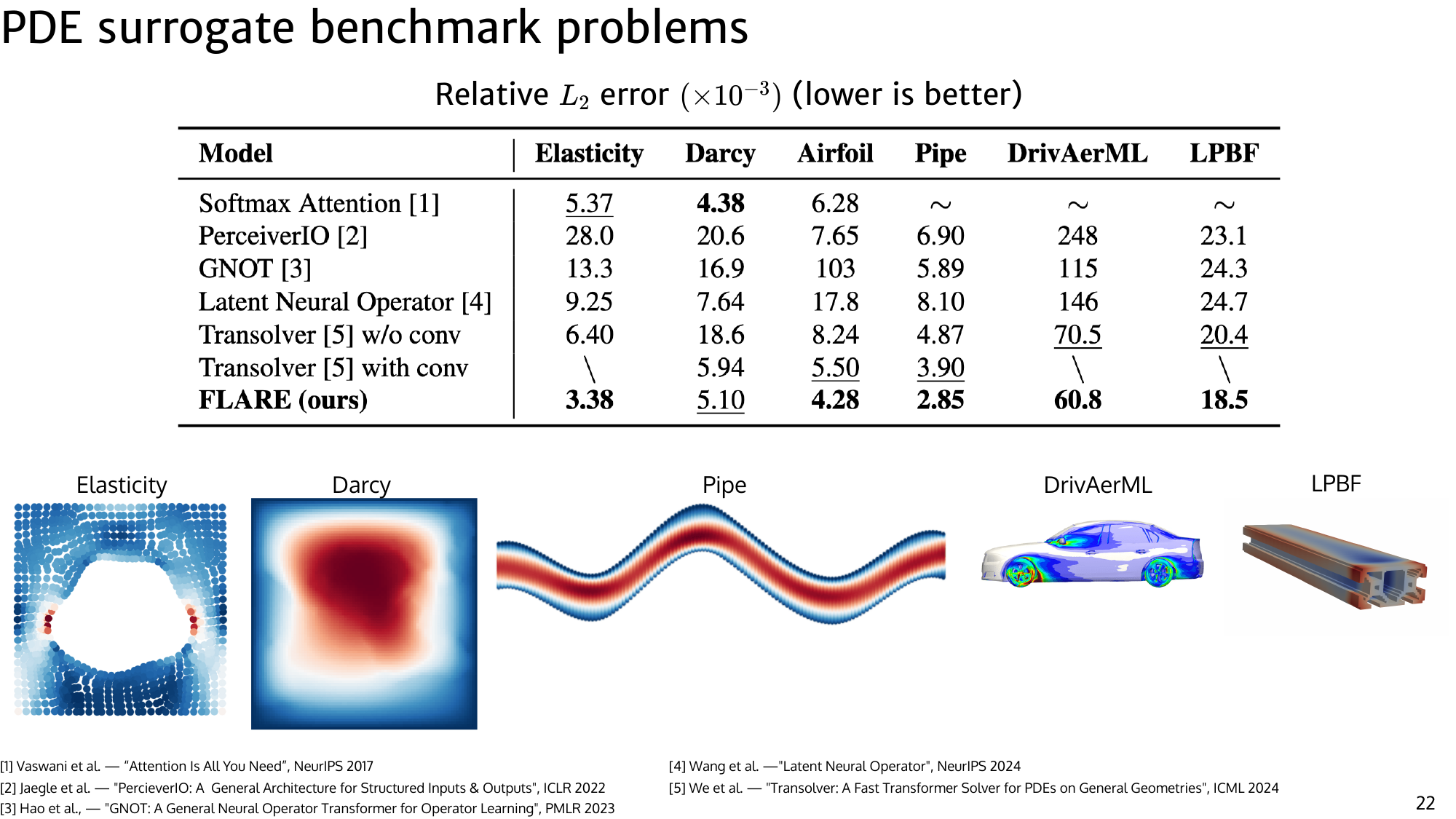
FLARE enables million-token training on a single GPU while maintaining strong accuracy on PDE surrogate tasks. The key improvement is not only asymptotic scaling but a practical runtime and memory profile that allows end-to-end training.

Slide 21: Low-rank token communication

On sequence benchmarks such as Long Range Arena, the operator remains competitive with other efficient transformer approaches, showing that the mechanism is broadly applicable beyond scientific data.

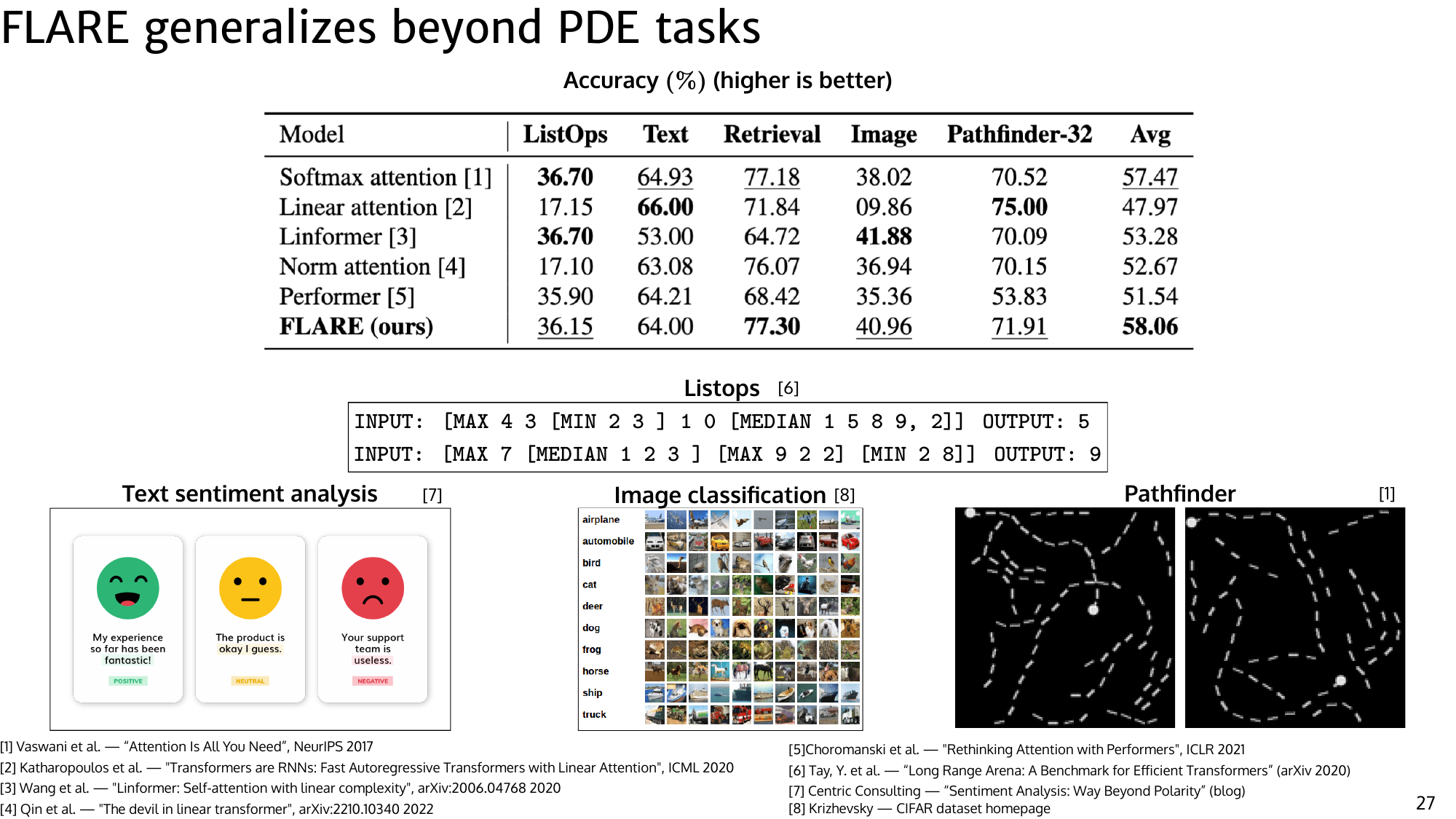
On sequence benchmarks, such as Long Range Arena, FLARE is competitive with efficient-transformer alternatives and maintains strong average accuracy, showing that the method is not restricted to PDE-only structure.

Slide 27: Long Range Arena results

Deep dive: why this design works

Understanding why FLARE works requires looking at the structure of the gather–scatter operator and how different design choices affect learning dynamics.

Gather–scatter as communication hubs

Each latent token acts as both a pooling hub and a routing hub. During encoding, it aggregates information from tokens that align with its query pattern. During decoding, it distributes that information back to tokens that match its key pattern. This creates a contraction–expansion communication structure that efficiently mixes global information.

Symmetric operators improve stability

The encode and decode steps are derived from the same query-key geometry, creating a structurally aligned operator. This symmetry reduces redundant parameterization and leads to more stable optimization compared to asymmetric variants.

Fixed queries provide a stable routing structure

Latent queries are learned but input independent. This gives a consistent communication basis across inputs, making the operator easier to optimize and interpret. The reduced query dynamism is compensated by expressive key and value encoders, which adapt routing patterns to each input.

Repeated global mixing is more effective than latent refinement

Empirically, allocating compute to repeated gather–scatter operations produces better performance than stacking heavy latent self-attention blocks. The benefit comes from repeatedly mixing global information rather than refining latent representations in isolation.

Independent latents across heads increase diversity

Allowing each head to have its own latent tokens produces more diverse communication pathways. Different heads learn complementary routing structures, improving accuracy and depth scaling.

Practical takeaways

Several design principles emerge:

  1. Use explicit low-rank communication rather than approximating local attention.
  2. Allocate compute to repeated global mixing.
  3. Keep routing pathways independent across heads.
  4. Use expressive key and value encoders when queries are fixed.

Closing thoughts

FLARE shows that scaling attention is not only about approximating softmax more efficiently. By rethinking attention as a communication operator, we can design mechanisms that preserve global information flow while dramatically reducing cost.

The broader lesson is that many large-scale problems have structure that can be exploited. Low-rank communication is one way to capture that structure without sacrificing flexibility, opening the door to practical million-token models on modest hardware.